都知道，在求解三角形中“逆等线”的相关动态问题时，首先要确准其的几个几何要素：①两逆等线段的交线的夹角大小，②两线段中的动点和定点及定点间线段长度，③两线段比值（加权数值）；然后对具体条件进行适当变换，如：平移、作外接圆、构作相似等方法求解；最后也可以试一试最底层的方法：作“旋转中心”。现举例几题，大家一起来说说：
【例一】（如图）在Rt△ABC中，斜边AC=2，∠C=60º，点E、F分别为边AC、CB上动点，连AF、BE交于点Q，且∠AQB=60º，求EF最小值
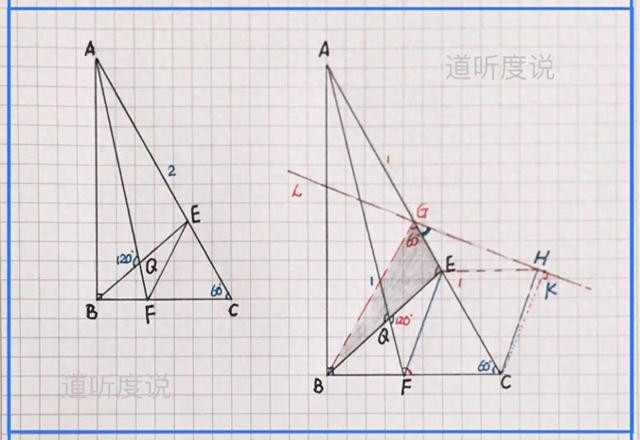
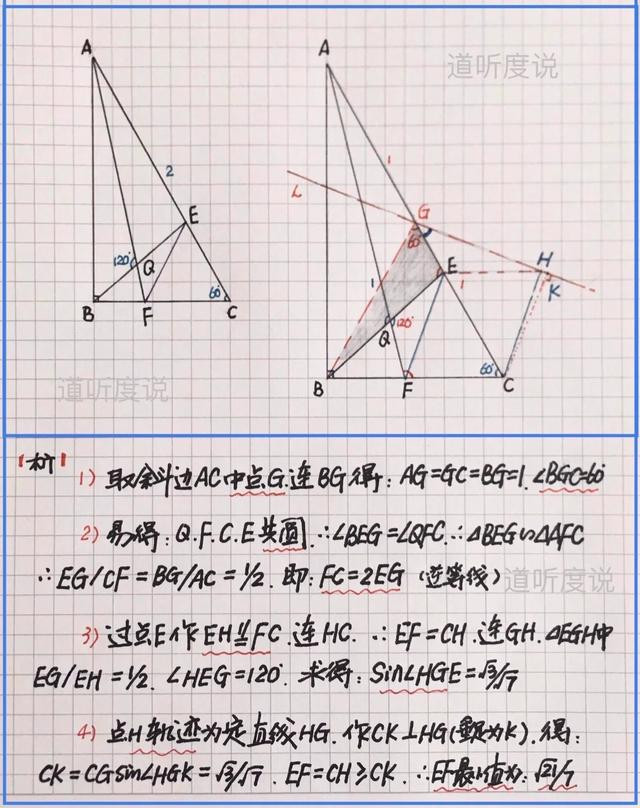
【分析】先取AC中点G连BG，正△GBC，易得GE=FC/2（巧造△GBC中的“逆等线”），动点E与F，定点G与C且GC=1，夹角∠BCG=60º；然后通过平移化双动点为单动点，同时得动点的轨迹…具体求解过程如下：
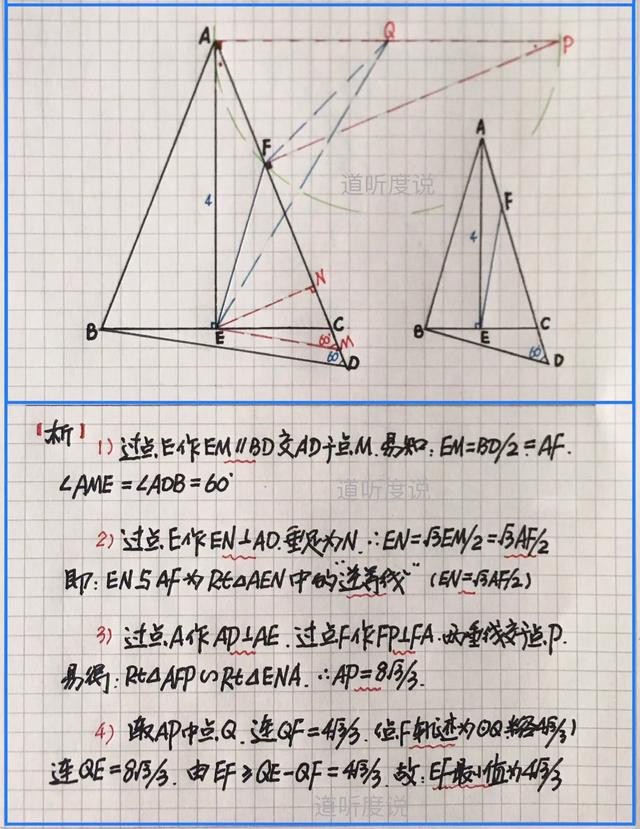
【例二】（如图）△ABC中，AB=AC，底边BC上高线AE=4，点F、D在射线AC上，且满足：∠ADB=60º，BD=2AF，求EF的最小值
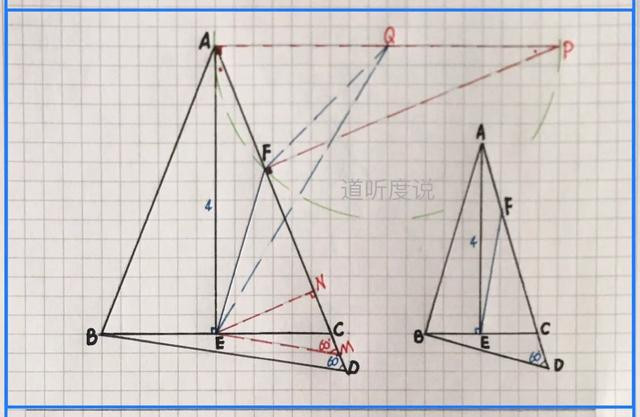
【分析】知：BD=2AF为△ABD中的“逆等线”，但两定点AB间线段长度不知，所以进行逆等线转化。作EM∥BD得AF=EM，其为△AEM中的逆等线，定线段AE=4，夹角为60º；然后利用作“三垂直”方法造相似得动点轨迹…具体求解过程如下：
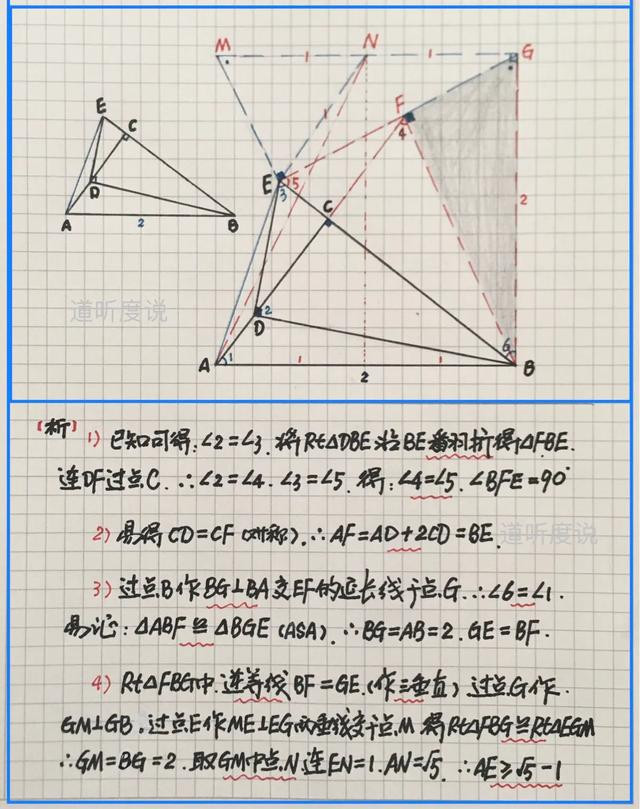
【例三】（如图）Rt△ABC中，斜边AB=2，射线AC上一点D，作DE⊥DB交射线BC于点E，且AD＋2CD=BE，求AE的最小值
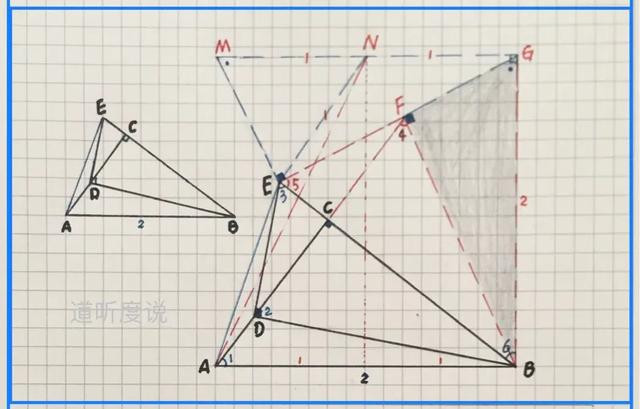
【分析】此题关键是利用（AD＋2CD）=BE。先将Rt△BED沿BE翻折，易得AF=BE；然后构作△ABF≌△BGE得BF=GE，其为Rt△BGF中的“逆等线”，两定点BG=2，两动点F与E，逆等线交角为90º；最后利用“三垂直”定动点轨迹…具体求解过程如下：
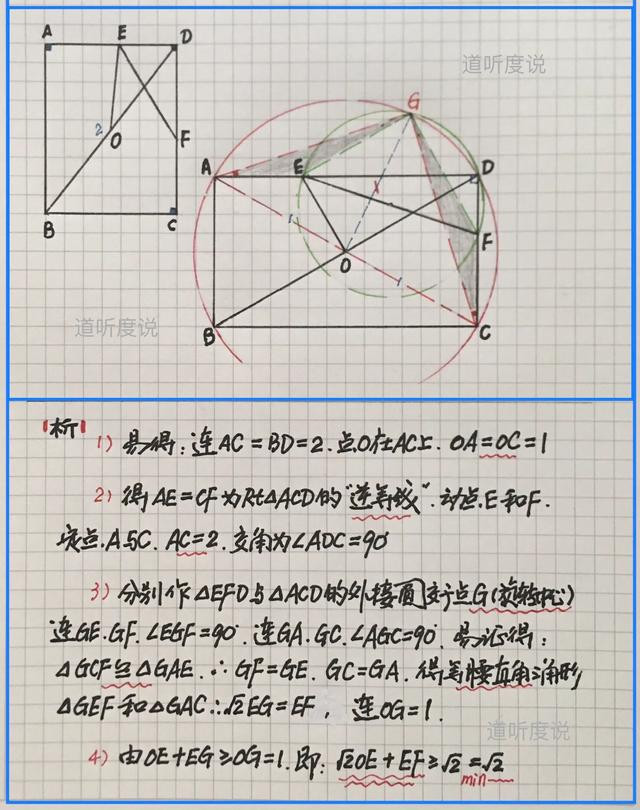
【例四】（如图）矩形ABCD中，点O为对角线BD的中点，BD=2，点E、F分别在射线AD、CD上，且AE=CF，求（√2OE＋EF）最小值
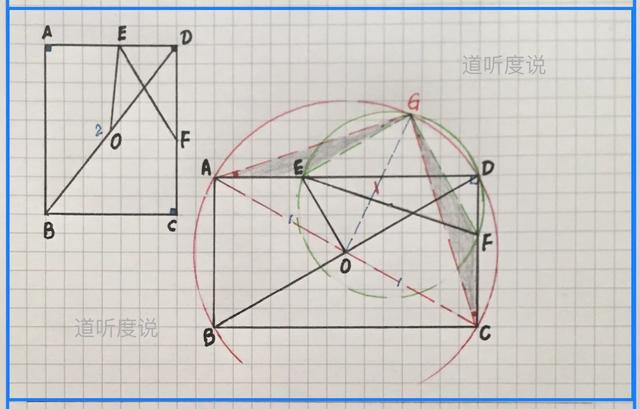
【分析】首先连AC=2过点O，得AE=CF为△ACD中的逆等线，动点E与F，定点A与C且AC=2，逆等线段交角为∠ADC=90º；然后分别作△EFD和△ACD的外接圆交于点G（旋转中心），得两个等腰直角三角形；最后导角寻边得…具体求解过程如下：
以上几例之分析，“道听度说”供参考。
新玺配资-短线配资平台-网络配资平台-股票配资中心提示：文章来自网络，不代表本站观点。
- 上一篇：西藏炒股配资〖佳方汇集〗《去痣方》月入超万
- 下一篇：没有了
